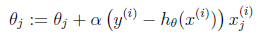点击的概率可以很自然地用条件概率来表达,given a(广告),u(用户), c(页面),p of click。我们可以用统计来预测点击率,我个人计为Regression比Ranking的方法更合适,我们知道在搜索中,Ranking的方法被广泛地研究,利用机器学习的方法得到更好的排序结果。但我们知道广告的排序是根据eCPM,所以,广告的排序并不能仅考虑CTR,因为eCPM还要考虑Bid,换言之,对广告网络而言,竞价广告系统需要准确地估计CTR。,如果是对DSP而言,对点击率的预测要求就更高了,因为DSP需要同时估计CTR和点击价值,CTR 和点击价值决定了DSP出价,即是向Exchange报的出价。
逻辑回归
Click的概率是服从Bi-nominal分布的,它的取值只能是0或1,我们很自然的想法就是用Logistic Regression模型。虽然有很多其它更Fancy的算法,但工程中常常使用的恰是这种简单的模型。
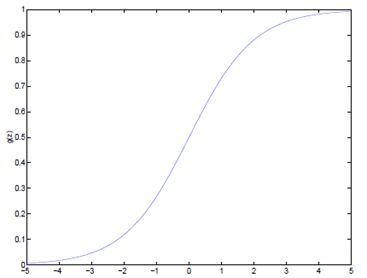
如果我们忽略二分类问题中y的取值是一个离散的取值(0或1),我们继续使用线性回归来预测y的取值。这样做会导致y的取值并不为0或1。逻辑回归使用一个函数来归一化y值,使y的取值在区间(0,1)内,这个函数称为Logistic函数(logistic function),也称为Sigmoid函数(sigmoid function)。
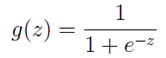
逻辑回归表达式
逻辑回归本质上是线性回归,只是在特征到结果的映射中加入了一层函数映射,即先把特征线性求和,然后使用函数g(z)将最为假设函数来预测。g(z)可以将连续值映射到0到1之间。线性回归模型的表达式带入g(z),就得到逻辑回归的表达式:
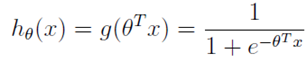
表达式就转换为:
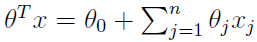
分类
现在我们将y的取值 通过Logistic函数归一化到(0,1)间,y的取值有特殊的含义,它表示结果取1的概率,因此对于输入x分类结果为类别1和类别0的概率分别为:

对上面的表达式合并一下就是:

梯度上升
得到了逻辑回归的表达式,下一步跟线性回归类似,构建似然函数,然后最大似然估计,最终推导出θ的迭代更新表达式。
我们假设训练样本相互独立,那么似然函数表达式为:
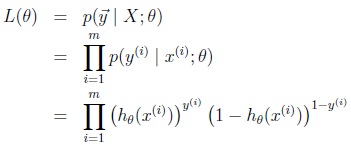
同样对似然函数取log,转换为:
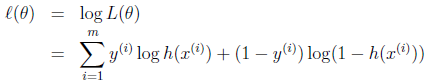
转换后的似然函数对θ求偏导,在这里我们以只有一个训练样本的情况为例:
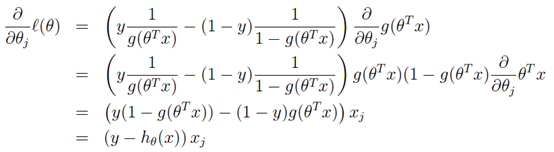
这个求偏导过程第一步是对θ偏导的转化,依据偏导公式:y=lnx y'=1/x。
第二步是根据g\(z\)求导的特性g'\(z\) = g\(z\)\(1 - g\(z\)\) 。
第三步就是普通的变换。
这样我们就得到了梯度上升每次迭代的更新方向,那么θ的迭代表达式为: